不确定性原理查看源代码讨论查看历史
模板参数错误!(代码34)
|
 |
于量子力学里,不确定性原理(uncertainty principle,又译测不准原理)表明,粒子的位置与动量不可同时被确定,位置的不确定性越小,则动量的不确定性越大,反之亦然。对于不同的案例,不确定性的内涵也不一样,它可以是观察者对于某种数量的信息的缺乏程度,也可以是对于某种数量的测量误差大小,或者是一个系综的类似制备的系统所具有的统计学扩散数值。 维尔纳·海森堡于1927年发表论文《论量子理论运动学与力学的物理内涵》给出这原理的原本启发式论述,希望能够成功地定性分析与表述简单量子实验的物理性质。这原理又称为“海森堡不确定性原理”。同年稍后,厄尔·肯纳德|Earl Kennard严格地数学表述出位置与动量的不确定性关系式。两年后,霍华德·罗伯森|Howard Robertson又将肯纳德的关系式加以推广。
类似的不确定性关系式也存在于能量和时间、角动量和角度等物理量之间。由于不确定性原理是量子力学的基要理论,很多一般实验都时常会涉及到关于它的一些问题。有些实验会特别检验这原理或类似的原理。例如,检验发生于超导系统或量子光学系统的“数字-相位不确定性原理”。对于不确定性原理的相关研究可以用来发展引力波干涉仪所需要的低噪声科技。
历史
1925年6月,海森堡在论文《运动与机械关系的量子理论重新诠释》(Quantum-Theoretical Re-interpretation of Kinematic and Mechanical Relations)里表述出矩阵力学。从此旧量子论渐趋式微,现代量子力学的时代正式开启。矩阵力学大胆地假设,经典的运动概念不适用于量子层级,束缚在原子内部的电子并不具有明确定义的轨道,而是运动于模糊不清,无法观察到的轨道,其对于时间的傅立叶变换[1] 只涉及到因量子跃迁而产生的可以被观察到的电磁辐射的离散频率。
海森堡在论文里提出,只有在实验里能够观察到的物理量才具有物理意义,才可以用理论描述其物理行为,其它都是无稽之谈。因此,他刻意避开任何涉及粒子运动轨道的详细计算,例如,粒子随著时间而改变的确切运动位置,因为,这运动轨道是无法直接观察到的,替代地,他专注于研究电子跃迁时,所发射出的电磁辐射的离散频率和强度。他计算出代表位置与动量的无限矩阵。这些矩阵能够正确地预测电子跃迁所发射出光波的强度。
同年6月,在阅读了海森堡的论文之后,马克斯·玻恩发现,海森堡的数学运算原来就是他在学生时代学到的矩阵微积分,另外,在分别表示位置与动量的两个无限矩阵之间存在著一种很特别的关系──正则对易关系,以方程式表示为:
- [x,\,p] = xp - px= i \hbar。
但是,他们并不了解这重要结果的意义,他们无法给予合理的诠释。
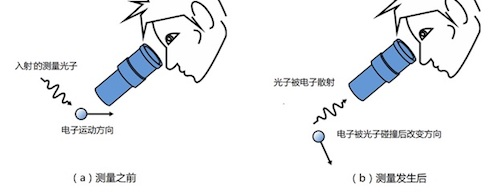
1926年,海森堡任聘为哥本哈根大学尼尔斯·波耳研究所的讲师,协助尼尔斯·波耳做研究。隔年,他发表了论文《论量子理论运动学与力学的物理内涵》(On the physical content of quantum theoretical kinematics and mechanics)。在这篇论文里,他严格要求遵守实证主义:只有在可以设定的实验环境下对于粒子的某种数量做测量,则这数量才具有物理意义,否则这数量不具有任何物理意义。他接著解释,任何实验测量都会遭遇误差,因此,这数量的物理意义也只能被确定至某种程度。例如,假设使用显微镜来测量粒子的位置,对于粒子的位置的测量会不可避免地搅扰了粒子的动量,造成动量的不确定性。海森堡紧跟著给出他的不确定性原理:越精确地知道位置,则越不精确地知道动量,反之亦然。不确定性原理能够直接地诠释位置与动量的正则对易关系:假若测量位置不会搅扰动量,测量动量不会搅扰位置,则测量位置与动量不需要顾虑到先后关系,位置与动量的正则对易关系会变为<math>[x,\,p] = xp - px=0</math>。 在这篇论文里,海森堡写出公式
- Delta x \Delta p\approx h。
这公式给出了任何位置测量所造成的最小无法避免的动量不确定值,但是他没有给予\Delta x和\Delta p<定义。在海森堡的芝加哥讲义里,他又进一步改善了这关系式:
- Delta x\Delta p\gtrsim h。
1927年,厄尔·肯纳德|Earl Kennard首先证明了现代不等式:
- Delta x\Delta p\ge\hbar/2;
其中,Delta x是位置标准差,Delta p是动量标准差,hbar是约化普朗克常数。
海森堡只给出关于高斯波包案例的不等式。
1929年,霍华德·罗伯森|Howard Robertson}}推导出基于对易关系的不确定关系式。